Entropiekodierung
Shortlinks
Allgemein
Die Entropiekodierung ist eine Art der verlustfreien Datenkompression. Die Entropiekodierung basiert darauf, dass Zeichen abgespeichert werden, wie beispielsweise ein Text. Dabei wir den einzelnen Zeichen eine unterschiedlich lange Folge von Bits zugeordnet.
Die Anzahl Bits, die für ein Zeichen verwendet werden wird dabei durch die Entropie bestimmt.
Entropiekodierer werden oft mit anderen Kodierern kombiniert und bilden dabei das letzte Stück in einer Datenkompression. Auf dieser Seite werden die Ereignisse als statistisch unabhängig betrachtet, was zwar eigentlich nicht der Fall ist, aber es wäre sehr schwierig die statistische Abhängigkeit auch noch einzubringen. Eine statistische Abhängigkeit wäre zum Beispiel unwahrscheinlich ist, dass in einem Wort zweimal der gleiche Buchstabe hintereinander steht.
Der Informationsgehalt
Der Informationsgehalt ist ein Mass dafür, wie viel Information in einer Nachricht übertragen wird. Dabei ist der Informationsgehalt eine logarithmische Grösse. Er wurde von Claude Elwood Shannon in seiner Informationstheorie formalisiert. Der Informationsgehalt bezeichnet die Anzahl Bits, die benötigt werden, um ein Zeichen, also eine Information darzustellen.
Definition
Der Informationsgehalt eines Zeichens wird über die Wahrscheinlichkeit, mit der es vorkommt, definiert und wird häufig auch als Auftrittswahrscheinlichkeit bezeichnet. Per Definition ist der Informationsgehalt eines Zeichens zn aus einer Symbolmenge Z = {z1, z2, z3, ... , zm} mit der Auftrittswahrscheinlichkeit pzn:
Wie aus der oben aufgeführten Formel ersichtlich ist, ist die Einheit desInformationsgehaltes davon abhängig, was wir als a definieren. Als a werden die möglichen Zustände genommen, die unsere Kodierung annehmen kann, also im Beispiel des Binäralphabetes wäre a = 2, mit den Zuständen 0 und 1. Beim Hexadezimalsystem wäre a = 16, da wir 16 verschiedene Zustände haben, um unser Zeichen zu kodieren. Im Allgemeinen kann die Einheit als Shannon (sh) bezeichnet werden. Dies hat sich aber nicht wirklich durchgesetzt, da im häufigsten Fall die Binärkodierung gewählt wird. In diesem Fall entspricht die Einheit einem Bit, welche auch verwendet wird.
Beispiel
Um den Begriff desInformationsgehaltes nach Shannons Informationstheorie zu verstehen muss man sich der herkömmlichen Bedeutung des Wortes Information entledigen. Denn der Informationsgehalt eines 500-seitigen Romans kann genau gleich sein, wie der Informationsgehalt der Ziffer 5, auch wenn die beiden Dinge etwas völlig anderes bedeuten. Wenn wir also ein Alphabet mit zwei verschiedenen Zeichen haben kann z1 der 500-seitige Roman sein und z2 die Ziffer 5. Dabei wird z1 mit der Binärziffer 0 und z2 mit der Binärziffer 1 codiert. Dieses zwei Nachrichten können also völlig frei gewählt werden und völlig unterschiedlich sein. Haben die beiden Nachrichten die gleiche Auftrittswahrscheinlichkeit, dann haben sie auch den gleichen Informationsgehalt. Der Informationsgehalt ist also gross, wenn eine unwahrscheinliche, also anders ausgedrückt unerwartete Information dargestellt wird.
Die Wahrscheinlichkeit
In der Formel für den Informationsgehalt kommt die Wahrscheinlichkeit pzn für ein Zeichen zn vor. Die Wahrscheinlichkeit ist muss nicht absolut, wie die Gegebenheit, dass zum Beispiel in der deutschen Sprache das Zeichen e sehr häufig vorkommt und somit sehr wahrscheinlich ist, sondern auch relativ. Wenn beispielsweise der Artikel 'der' als Zeichen genommen wird, dann ist die Wahrscheinlichkeit gross, dass ein Nomen oder ein Adjektiv folgt und die Wahrscheinlichkeit, dass ein Verb oder ein Pronomen folgt ist sehr klein. Mit einem Blick auf die Formel für den Informationsgehalt wird klar, dass der Informationsgehalt für ein Nomen oder ein Adjektiv klein und der Informationsgehalt für ein Verb oder ein Pronomen dementsprechend gross ist. Diese Wahrscheinlichkeit basiert aber auf statistischer Abhängigkeit. Deswegen wird nicht näher darauf eingegangen.
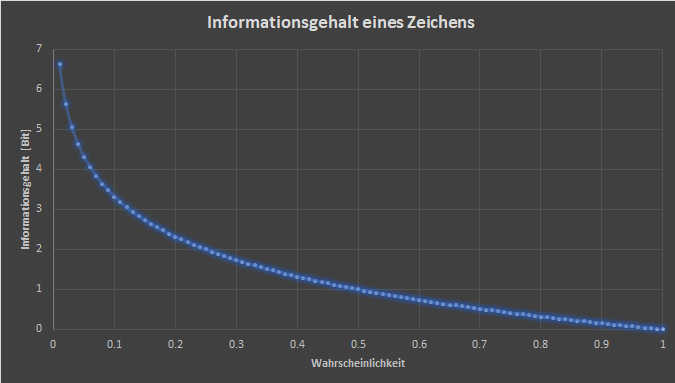
Die Grafik rechts oder oben zeigt den Informationsgehalt in Bits in Abhängigkeit der Wahrscheinlichkeit. Die Datenpunkte gehen dabei von einer Wahrscheinlichkeit von 0.01, also einem Prozent bis zu 1, also 100 Prozent, was natürlich einen Informationsgehalt von 0 Bits bedeuten würde. Die Schrittweite beträgt dabei 0.01, also ein Prozent.
Rechenbeispiel
In diesem Beispiel schauen wir uns an, wie viele Bit nötig sind, um das Wort 'Alleinsein' optimal binär zu kodieren. Dabei nehmen wir an, dass die einzelnen Zeichen (Buchstaben) statistisch unabhängig voneinander sind, dass man also nicht sagen kann, dass es unwahrscheinlich ist, dass nach einem Vokal nochmal ein Vokal folgt.
Zuerst müssen wir die einzelnen Wahrscheinlichkeiten der Zeichen berechnen, was einfach durch die Anzahl Vorkommnisse durch die Gesamtanzahl der Zeichen ausgerechnet werden kann.
Danach muss jeder einzelne Informationsgehalt mit der Formel aus der Definition, die oben steht, berechnet werden. Die einzelnen Informationsgehalte können nun addiert werden, um den gesamten Informationsgehalt der Nachricht zu finden.
Diese 25.22 Bits, die wir aus der Rechnung erhalten haben müssen wir nun aber noch aufrunden auf 26 Bits, da wir keine Bruchteile von Bits haben können. So kann das Wort 'Alleinsein' also mit 26 Bits optimal kodiert werden.
Die Entropie
Die Entropie in der Informatik wird als informationstheoretische Entropie nach Shannon bezeichnet und wurde, wie der Name bereits sagt zusammen mit dem Informationsgehalt von Claude Elwood Shannon definiert. Die Entropie wird mit einem grossen Eta Η dargestellt und hat (meistens) die Einheit Bit / Zeichen.
Definition
Die Entropie hängt stark mit dem Informationsgehalt zusammen. Dabei stellt sie den mittleren Informationsgehalt der verschiedenen Zustände, die eine Information einer Nachricht annehmen kann dar. Im binären Format wären die verschiedenen Zustände also 0 und 1, im lateinischen Alphabet wären es die Buchstaben von a bis z. Im lateinischen Alphabet gäbe es also 26 verschiedene Zustände, die für jede einzelne Information angenommen werden können. Der Mittelwert der Informationsgehalte berechnet sich nicht, wie wahrscheinlich erwartet aus der Summe aller Informationsgehalte geteilt durch die Anzahl der Informationsgehalte. Dabei stellt das Symbol pzn jeweils die Wahrscheinlichkeit des Zeichens yn dar aus der Menge aller möglichen Zeichen Ζ = {z1, z2, z3, ..., zm}.
Wenn wir es so machen würden hätten wir ein Problem mit Zeichen, die wenig vorkommen, also eine kleine Wahrscheinlichkeit und damit einen grossen Informationsgehalt haben. Das Problem damit wäre, dass alle Informationgehälter in der obigen Formel gleich behandelt werden. Damit hätte ein Zeichen, dass nur sehr wenig auftreten würde einen grossen Einfluss auf den durchschnittlichen Informationsgehalt in einem Text. Dies macht aber keinen Sinn, weswegen wir etwas einbauen müssen, womit das Vorkommen im Text berücksichtigt wird. Das können wir machen, indem wir von jedem Zeichen den Informationsgehalt mit der Wahrscheinlichkeit multiplizieren. Diese Produkte können dann zueinander addiert werden und wir erhalten den durchschnittlichen Informationsgehalt unserer Nachricht. Mathematisch dargestellt sieht es dann folgendermassen aus:
pz1 * I(z1) + pz2 * I(z2) + ... + pzm * I(zm) =
pz1 * log2(pz1) + pz2 * log2(pz2) + ... + pzm * log2(pzm) =
-
Falls wir eine Nachricht haben, die mehrere Informationen enthält, kann über die Entropie relativ einfach berechnet werden, wie viele Bits benötigt werden, um die Nachricht abzuspeichern. Dies können wir herausfinden, indem wir die Entropie mit der Anzahl der vorkommenden Zeichen multiplizieren.
Beispiel
Die Entropie eines Würfels mit sechs Seiten, die alle mit der gleichen Wahrscheinlichkeit gewürfelt werden können, lässt sich sehr einfach berechnen. Die Menge der Ergebnisse dieses Würfels sind: E = {1, 2, 3, 4, 5, 6}. Es liegen also 6 verschiedene Möglichkeiten vor, von denen jede mit gleicher Wahrscheinlichkeit gewürfelt werden kann. Die Wahrscheinlichkeit liegt somit bei p1 = p2 = ... = p6 = 0.1666... = 6-1. Wenn wir daraus den Informationsgehalt berechnen erhalten wir I = -log2(6-1) = log2(6). Dieser multipliziert mit der Wahrscheinlichkeit ergibt: 6-1 * log2(6). Wenn wir nun alle Informationsgehalte, multipliziert mit der Wahrscheinlichkeit zueinander addieren, dann erhalten wir die Entropie Η = 6 * 6-1 * log2(6) = log2(6).
Dabei fällt schnell auf, dass die Entropie genau dem Informationsgehalt eines einzelnen Wurfes mit dem Würfel entspricht. Diese Entdeckung macht auch Sinn, da die Entropie per Definition den mittleren Informationsgehalt eines Wurfes darstellen soll. Da alle Informationsgehälter genau gleich sind muss der mittlere Informationsgehalt jedem einzelnen Informationsgehalt entsprechen.
Rechenbeispiel
In diesem Beispiel wollen wir die Entropie des Satzes 'Ich mag die Entropiekodierung' berechnen, wobei wir als erlaubte Symbole die Buchstaben verwenden, die im Satz vorkommen und jeden einzelnen Buchstaben als einzelne Information ansehen. Es kommen im Satz also 15 verschiedene Symbole, die 26 Informationen darstellen vor. Gross- und Kleinschreibung, sowie die Leerzeichen zwischen den Wörtern werden dabei ausser Acht gelassen. Zuerst müssen wir also die Wahrscheinlichkeit durch das Vorkommen der einzelnen Buchstaben bestimmen.
Danach muss nach der Definition der Entropie die Summe aller Informationsgehalte multipliziert mit den Wahrscheinlichkeiten der Zeichen ausgerechnet werden. Dafür müssen wir die Entropie für jedes einzelne Zeichen berechnen und danach durch die Summe davon die Gesamtentropie.
Die Nachricht, die aus dem Satz 'Ich mag die Entropiekodierung' besteht hat also einen mittleren Informationsgehalt von 5.04 Bit / Zeichen. Dabei wurden jedoch die Leerzeichen weggelassen, da diese nicht im vorgegebenen Alphabet enthalten sind und somit eine Wahrscheinlichkeit von 0 haben und nichts zur Entropie beitragen. Der Speicherplatz, der für diesen Satz bei einer optimalen Entropiekodierung gebraucht berechnet sich aus der Anzahl der Zeichen multipliziert mit der Entropie: 5.04 Bit / Zeichen * 15 Zeichen = 75.58 Bit => 76 Bit. Dieser Wert entspricht genau der Summe der einzelnen Informationsgehalte.
Beispielcode in Python
Dies ist ein in Python geschriebener Beispielcode:
# Nötiger Import
import math
# Gibt die Entropie einer Information I (String) über einem Alphabet A (Liste) aus
def entropy(I, A):
# Die Entropie wird direkt als Fliesskommazahl definiert
entropy = 0.0
info = 0
# Jedes Element des Alphabets trägt zur Entropie bei
for i in range(len(A)):
# Zählt wie viel ein Zeichen im String vorkommt
counter = float(I.count(I[i]))
# Definiert die Wahrscheinlichkeit eines Zeichens
p = counter / len(A)
# Definiert den Informationsgehalt des Zeichens zum Logarithmus der Basis 2, sofern die Wahrscheinlichkeit < 0
if p > 0:
info = - math.log(p) / math.log(2)
# Addiert den Teil zur Gesamtentropie
entropy += p * info
return entropy
Maximale Entropie
Die Entropie einer Nachricht, die aus n Zeichen besteht, kann nicht beliebig gross sein. Dabei kann ein Maximum bestimmt werden, nämlich wenn jedes Zeichen in der Nachricht nur einmal vorkommt, wie beispielsweise in einem Isogramm. Ein Beispiel dafür wäre das Wort 'Dialektforschung'. Dieses Wort besteht aus 16 Buchstaben, also 16 Informationen. Nun wollen wir das gesamte lateinische Alphabet mit 26 Buchstaben verwenden. So haben wir also 16 Buchstaben, die die gleiche Wahrscheinlichkeit haben und die restlichen zehn Buchstaben haben auch die gleiche Wahrscheinlichkeit:
Wenn wir die Formel für die Entropie der Information 'Dialektforschung' anwenden erhalten wir:
Wenn wir das ganze noch vereinfachen und dabei den Grenzwert
Für den allgemeinen Fall kann man aus der Lösung der Obenstehenden Rechnung schliessen, dass die maximale Entropie bei einem Alphabet mit N Elementen und einer Nachricht, die Q Informationen beinhaltet mit der Darstellung über dem Binärsystem mit folgender Formel berechnet werden kann:
Die Redundanz
Die Redundanz bezeichnet die Informationen aus einer Informationsquelle, die mehrfach verwendet werden. Somit kann eine redundante Informationseinheit ohne Informationsverlust weggelassen werden. Somit ist der Teil einer Nachricht, der keine Information enthält, redundant. Die Redundanz ist eine Logarithmische Grösse und zeigt an, wie viel Mal kürzer eine Kodierung sein könnte.
Berechnung
Die Redundanz kann aus der Differenz zwischen der maximalen Entropie einer Quelle und der Entropie derselben Quelle berechnet werden. Damit muss kann sie minimal 0 sein, da die Entropie die maximale Entropie nie überschreiten kann. Da es sich um eine Subtraktion handelt erhält die Redundanz die gleiche Einheit wie die Entropie: Bit / Zeichen.
Rechenbeispiel
Dieses Rechenbeispiel berechnet die Redundanz eines Textes, der mit dem lateinischen Alphabet: Z = {a, b, c, ..., z} geschrieben wurde und somit 26 verschiedene Zeichen enthält. Für die Auftrittswahrscheinlichkeit dieser Zeichen wurden die Werte von Wikipedia, in der Spalte der deutschsprachigen Texte verwendet. Die Gross- und Kleinschreibung, sowie die Leerzeichen werden dabei nicht berücksichtigt, da diese die ganze Sache nur noch unnötig kompliziert machen würden.
Um die Redundanz zu berechnen müssen wir zuerst die Entropie und die maximale Entropie des Textes berechnen. Der Text erreicht seine maximale Entropie, wenn alle Zeichen die gleiche Auftrittswahrscheinlichkeit haben, also gleich viel vorkommen. Somit ergibt sich:
-(0.0545 * log2(0.0545) + 0.0175 * log2(0.0175) + 0.0337 * log2(0.0337) + 0.0511 * log2(0.0511) + 0.1689 * log2(0.1689) + 0.0128 * log2(0.0128) + 0.0376 * log2(0.0376) + 0.0526 * log2(0.0526) + 0.0851 * log2(0.0851) + 0.0018 * log2(0.0018) + 0.0151 * log2(0.0151) + 0.0377 * log2(0.0377) + 0.0222 * log2(0.0222) + 0.1042 * log2(0.1042) + 0.0311 * log2(0.0311) + 0.0063 * log2(0.0063) + 0.0001 * log2(0.0001) + 0.0714 * log2(0.0714) + 0.0624 * log2(0.0624) + 0.0608 * log2(0.0608) + 0.0340 * log2(0.0340) + 0.0089 * log2(0.0089) + 0.0164 * log2(0.0164) + 0.0002 * log2(0.0002) + 0.0007 * log2(0.0007) + 0.0127 * log2(0.0127))
≈ 4.0646
Ηmax =
≈ 4.7004
Nun müssen wir die Differenz dieser beiden Werte bilden und erhalten den Wert für die Redundanz von (grossen, damit die Auftrittswahrscheinlichkeit gut angenähert werden kann) in Deutsch geschriebenen Texten.
0.6358
Wir haben also eine Redundanz von 0.6358 Bit pro Zeichen in deutschsprachigen Texten. Das bedeutet, dass wir mit einer optimalen Entropiekodierung im Durchschnitt 0.6358 Bit pro Zeichen an Daten einsparen können. Dies scheint zwar wenig, aber wenn wir nun Beispielweise einen Bericht mit 10'000 Buchstaben haben, dann können wir 10'000 Zeichen * 0.6358 Bit / Zeichen = 6358 Bit einsparen, was schon ein beträchtlicher Betrag sein kann. Eine Entropiekodierung ist also sinnvoll für Situationen mit grosser Redundanz, wäre aber zum Beispiel sinnlos für die Aufzeichnung der Würfe eines Würfels, bei dem jede Möglichkeit die gleich Auftrittswahrscheinlichkeit hat, womit die Redundanz 0 beträgt und eine Entropiekompression keine Daten einsparen könnte.
